2019-07-21

シュレディンガー(Schrödinger)方程式の導出①

[物理化学]量子化学

Hirokikiです。

今回はSchrödinger方程式の導出について勉強していきましょう。

Schrödinger方程式の代表的な式の形は

$\Large\hat{H}\Psi=E\Psi\tag{1}$

かと思います。式(1)の $\hat{H}$ はハミルトニアン演算子、 $\Psi$ は波動関数、Eはエネルギーです。

式自体はよくみるものの、どこからこの式が導かれたのかが自分自身よくわからず、同じような疑問を持っている方が自分以外にもきっといるのではと考え、大まかな導出をこの記事でやっていきます。

式の導出には、まず重要な2式を導出し、その2式を組み合わせてSchrödinger方程式を導出します。この記事では、仮定として1次元での場合とします。その重要な2式は式(2)と式(3)です。

$\Large{E}=\dfrac{p^2}{2m}+V(x)\tag{2}$

$\Large\dfrac{d^2X(x)}{dx^2}+\dfrac{4\pi^2}{\lambda^2}=0\tag{3}$

ここでSchrödinger方程式の対象は光や電子などの量子ですが、量子は「粒子と波動の二重性」を持ちます。つまり式(2)は粒子性を、式(3)は波動性を表す方程式であり、それらをどちらも満たす方程式がSchrödinger方程式となります。

これから導出をしていきますが、ひとつの記事で最後まで導出すると長くなるため、順々に導出していきます。式(2)はこの記事で導出し、次の記事以降で式(3)の導出、Schrödinger方程式の導出をまとめていきます。

それではここから式(2)の導出をしていきましょう。式(2)は「粒子の全エネルギー」を表しています。

粒子の全エネルギーの一般的な式の形は

$\Large{E}=\dfrac{1}{2}mv^2+V(x)\tag{3}$

かと思います。一項目が運動エネルギー、二項目がポテンシャルエネルギーです。

ここで、粒子の運動量は

$\Large{p}=mv\tag{4}$

です。式(4)を式(3)に代入し、

$\Large{E}=\dfrac{p^2}{2m}+V(x)\tag{2}$

が得られます。

最後に、後々のため式を変形します。

$\begin{aligned} \Large{E}&=\Large{\dfrac{p^2}{2m}+V(x)}\\ \Large{E-V(x)}&=\Large{\dfrac{p^2}{2m}}\\ \Large{p^2}&=\Large{\{2m(E-V(x)\}}\\ \end{aligned}\tag{5}$

今回はここまでです。お疲れ様でした。

[参考文献]

これからはじめる量子化学―物理・数学のキホンからよくわかる! ―

作者: 辻和秀
出版社/メーカー: オーム社
発売日: 2013/08/24
メディア: 単行本（ソフトカバー）
この商品を含むブログを見る

2019-05-28

Newman投影式

[大学化学]有機化学

今回は、Newman投影式について勉強していきましょう。

本題に入る前にまず、押さえておきたいのですが

分子は本来、3次元構造をとるということを確認したいです。

高校化学の教科書の有機化学のところを改めて確認してみると、あまり3次元的なことには触れておらず (今は違うかも) 、それよりかは物質Aと物質Bを反応させると物質Cができるみたいな内容が多い印象だったのでここから確認しました。

そんなの常識、という方は申し訳ありませんでした。

そんなの知らなかった、という方は、有機化学のイメージが変わると思うので、ぜひ一緒に勉強していきましょう。

(一緒に勉強していけばもしかしたら、反応条件と反応原子をただ暗記する有機化学のイメージも変わるかも?)

では本題に入りましょう。

この記事では、Newman投影式がどのようなものなのかについて勉強していきます。

説明に使う分子例として、エタンを例に話を進めていきます。
エタンの構造を3次元的に書くと図1に示します。

f:id:Naporeon:20190528210418p:plain — 図1. エタンの3次元構造

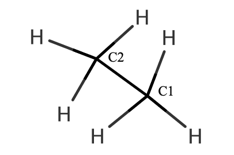
図1のエタンの3次元的な表し方を「木びき台表示」というらしいです。

また、より一般的な3次元的な表し方は、「くさび型表示」があります。

(これは大学受験の問題で見たことがあるので知っている方も多いかもしれません。)

この記事では図1の手前の炭素をC１、奥の炭素をC2とします。

図1のようなエタンは全て単結合であり、同時にσ結合です。σ結合は軸対称性の結合なので、単結合は回転できます。

ここで、単結合周りの回転による原子配列の違いは、「立体配座」と呼ばれ、あるとりえる配座がもつエネルギーが極小となる立体配座は「配座異性体」と呼ばれます。

この、配座異性体を表現するのに「Newman投影式」があります。

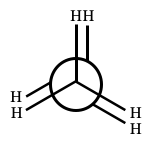
例を図2で示します。

f:id:Naporeon:20190528205735p:plain — 図2. エタンのNewman投影式

図2のように、C1-C2結合の延長線上からみて、2つのCを1つの円として表現します。C1のC-H結合は、この円の中心に届く線で表し、C2のC-H結合は、円の周囲から出ている線で表現します。

また、単結合は回転できるので、 C2を60°右に回転した配座異性体を図3に示します。

f:id:Naporeon:20190528205842p:plain — 図3. C2を60°右に回転したNewman投影式

ここで、考えついているかもしれませんが、図2と図3で、エネルギー的に低く安定な配座異性体は図3です。

なぜかというと、図2では、C-H結合が互いに出来るだけ離れている配座 (ねじれ型配座) であるのに対し、図3ではC1とC2の、互いのC-H結合が近づき、重なり合っています (重なり型配座)。

C-H結合が重なることで、C1に結合しているHとC2に結合しているHとの「立体障害」が発生し、図3の方が相対的に不安定な配座となります。

この、何もエネルギーを使わなければ、より安定な方を取りやすいというのは、分子だけの世界ではなく、色々現実世界でも言えるかなと思います。

例えば部屋の掃除など、エネルギーを使わなければどんどん散らかっていきますよね。

(これはよくエントロピーの例で出される例ですが笑)

最後に、Cを回転していった時に、エネルギーがどのような関数になるのかを見ていきましょう。図4に示します。

f:id:Naporeon:20190528205936p:plain — 図4. エタンのC2を60°右に回転したことによるエネルギーの推移

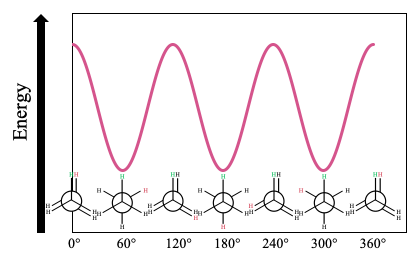
図4の横軸が、C2の炭素の右回りの回転角度、縦軸が回転角度に対応するエネルギーです。

見てもらったらわかる通り、sinやcosのような曲線になります。また、重なり型配座をとる時にエネルギーが極大になり、ねじれ型配座の時に極小を取ることがわかります。

まとめ

Newman投影式は、配座異性体を表現する方法である。

今回は以上です。

最後まで読んでくださりありがとうございます。

2019-05-19

共鳴構造

[大学化学]有機化学

Hirokikiです。

今回は共鳴構造について学んでいきましょう。

共鳴構造は、一言で言うと電子が局所的にどの原子に存在しているのかを表した構造のことです。

酢酸イオンを用いて説明していきたいと思います。

酢酸イオンの共鳴構造を図1に示します。

f:id:Naporeon:20190519102555p:plain — 図1. 酢酸イオンの共鳴構造

共鳴は両矢印を使って表します。

(ここで「平衡」とは矢印の表記と意味が異なるので、注意です。)

図1の左と右の構造、ひっくり返せば同じ構造じゃないか？なにが違うのか？と思うかもしれません。

その疑問はある意味正しいのですが、この例が表していることは、酢酸イオンは2種類の共鳴 (極限) 構造を持つということです。

つまり、Oに負電荷を帯びているのは、極端に電荷が偏った構造を考えた仮想的な構造であり、本来はO, C, O間に負電荷が非局在化しているということです。

この電荷が局在化している、非局在化しているという考え方は高校化学では扱わないので理解しづらいかもしれませんが、重要な考え方です。

また、図1の左の構造から右の構造、もしくは右の構造から左の構造に変化する際に結合種が変化していますが、それの表し方としては「巻矢印」を使います。

図1を使うとこんな感じです。図2に示します。

f:id:Naporeon:20190519102715p:plain — 図2. 巻矢印を使った酢酸イオンの共鳴構造

巻矢印を文字で説明しにくいのですが、一つの矢印で2電子の移動を表現しています。

図2の左の酢酸イオンだと、初めに下のOの非共有電子対 (電子が2個) は3つありますが、その内一つの非共有電子対が単結合のところに降りて、二重結合を形成します。

次に、中央のCは4本の結合しか作れないので、電子が押し上げられるように、上のOとの二重結合を解消して単結合になり、余った電子対はOに乗って、Oは形式電荷として負の電荷を帯びます。

この、電荷が非局在化していることを図3のように表したりもします。

f:id:Naporeon:20190519103651p:plain — 図3. 酢酸イオンの電子の非局在化を表した構造

図3の点線が、O, C, O間で電子が非局在化していることを表しています。

最後に、分子中の電子の局在化、非局在化を3次元で表すとどうなるのかについて触れます。

それが静電ポテンシャルマップといわれるものです。

図4に酢酸の例を示します。
(本当はここで、酢酸イオンの電子の非局在化を示したかったのですが、フリーソフトだと正しく描写できず、やむなく酢酸としました。申し訳ありません。)

f:id:Naporeon:20190519103838p:plain — 図4. 酢酸の静電ポテンシャルマップ

図4は各原子軌道を重ね合わせた混成軌道を表しています。

見方としては、赤に近い色程、その原子上に電子が多く存在していることを表し、紫に近い色程電子が存在しないことを表しています。

つまり図4で言えば、Oに電子が多く存在し、HやCにはあまり電子が存在していないことがわかります。

まとめ

共鳴構造は、電子の局在化を表した構造である。

今回は以上です。

最後まで読んでくださりありがとうございます。

2019-05-11

形式電荷

[大学化学]有機化学

今回は、形式電荷について勉強していきましょう。

形式電荷とは、分子中の原子毎の形式的な電荷です。

分子の形式電荷を調べることで、分子中のどの原子が電子豊富や電子不足になっているかがわかります。

それが分かることで、電子のやり取りが行われる化学反応の手がかりにも役立ちますし、共鳴という概念でも使う考え方です。

形式電荷は次の式1のような一般式によって求まります。

f:id:Naporeon:20190511154440p:plain

文字での説明はここまでです。

ここからは実際の分子の例で確認していきましょう。

図1にH2O, CH4, DMSOの分子を示しました。

f:id:Naporeon:20190511155113p:plain — 図1. 分子例

図1の分子のそれぞれの原子について形式電荷を求めてみましょう。

f:id:Naporeon:20190511155025p:plain

まとめ

形式電荷は、分子中の原子毎の形式的な電荷であり、電荷は電子に関する一般式によって求めることができる。

今回は以上です。

最後まで読んでくださりありがとうございます。

2019-04-23

軌道を用いた共有結合の記述

[大学化学]有機化学

前回軌道について扱いましたが、今回は軌道を使ってどのように共有結合を表すのかについて勉強していきましょう。

まず復習ですが、共有結合がどういうものだったかというと互いの原子が同じ数ずつ電子を出し合って電子対を作り、共有することで結ぶつく結合でした。水素分子を例に、図で表すと図1です。

f:id:Naporeon:20190423214413p:plain — 図1. 高校化学までの共有結合の表し方

さて、軌道を用いた共有結合の記述には、原子価結合法と分子軌道法の2種類の考え方があります。

どちらもとても重要な考え方ですが、区別がつけにくく、それぞれの考え方を混同しやすいです。

なので表1にまとめてみました。

f:id:Naporeon:20190423214700p:plain — 表1. 原子価結合法と分子軌道法の違い

図2次に、原子価結合法と分子軌道法の水素分子の例を図2、図3にそれぞれ示します。

f:id:Naporeon:20190423214817p:plain — 図2. 原子価結合法による水素分子

f:id:Naporeon:20190423214913p:plain — 図3. 分子軌道法による水素分子

図2の原子価結合法は、1s電子が1個ずつ入った2つの軌道が重なり合ってH-H結合を形成すると考えます。一方図3の分子軌道は、分子になることで形成される1s軌道よりもエネルギーが低い(安定な)結合性軌道と、1s軌道よりもエネルギーが高い(不安定な)反結合性軌道の2つの軌道を考えます。そのうちより安定な結合性軌道に電子が2つ入るという考え方です。

水素分子を例で示したものの、水素分子は単純な分子なため、あまり違いは無いように思えるかもしれないのですが、複雑な分子になるほど差は顕著になります。

締め

共有結合を記述するための考え方は原子価結合法と分子軌道法がある。

原子価結合法は、電子が入った軌道が互いに重なり合うことで結合が形成される、という考え方。

分子軌道法は、エネルギーが低い結合性軌道とエネルギーが高い反結合性軌道を考える方法である。

今回は以上です。

最後まで読んでくださりありがとうございます。